Matematica: i due caratteri della funzione - crescenza e decrescenza

Si definisce funzione f di dominio A e codominio B una relazione che associa a ogni elemento di A uno e un solo elemento di B. L’elemento y є B che è associato a x є A è detto immagine di x. Si dice che x è la variabile indipendente della funzione, mentre y è la variabile dipendente.

Esempio: le relazioni rappresentate nella figura (a) sono funzioni, mentre le relazioni rappresentate nella figura (b) non lo sono.

                       

                                          (a)                                 (b)

                     

Sia I un sottoinsieme del dominio della funzione y = f(x):

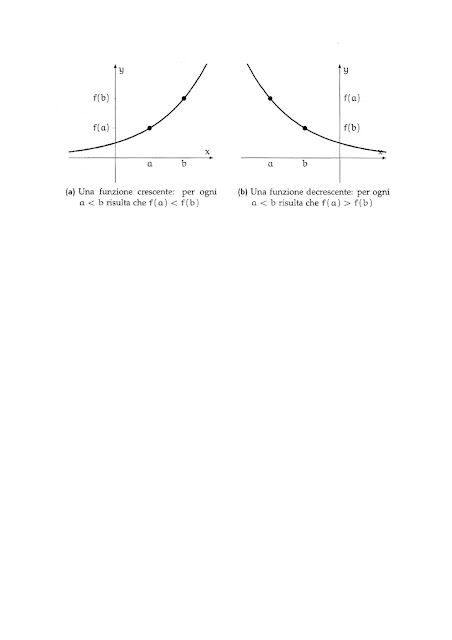
·        f si dice crescente in I se a < b implica f(a) < f(b) per ogni a,b є I
·        f si dice decrescente in I se a > b implica f(a) > f(b) per ogni a,b є I

Cominciamo a evidenziare un legame tra il segno della derivata di una funzione e gli intervalli in cui la funzione cresce o decresce.

Lo strumento impiegato per individuare gli intervalli in cui una funzione è crescente o decrescente: basta calcolare la derivata prima e studiarne il segno, risolvendo la disequazione f’ (x)≥ 0.

 Sia f una funzione derivabile in un intervallo I:

·        Se f’ (x) > 0 per ogni x є I, allora f è crescente in I

·        Se f’ (x) < 0 per ogni x є I, allora f è crescente in I